Grüneisen parameter
The Grüneisen parameter, γ, named after Eduard Grüneisen, describes the effect that changing the volume of a crystal lattice has on its vibrational properties, and, as a consequence, the effect that changing temperature has on the size or dynamics of the lattice. The term is usually reserved to describe the single thermodynamic property γ, which is a weighted average of the many separate parameters γi entering the original Grüneisen's formulation in terms of the phonon nonlinearities.[1]
Contents |
Thermodynamic definitions
Because of the equivalences between many properties and derivatives within thermodynamics (e.g. see Maxwell Relations), there are many formulations of the Grüneisen parameter which are equally valid, leading to numerous distinct yet correct interpretations of its meaning.
Some formulations for the Grüneisen parameter include:
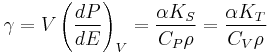
where V is volume, 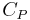 and
and 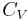 are the principal (i.e. per-mass) heat capacities at constant pressure and volume, E is energy, α is the volume thermal expansion coefficient,
are the principal (i.e. per-mass) heat capacities at constant pressure and volume, E is energy, α is the volume thermal expansion coefficient, 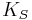 and
and 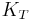 are the adiabatic and isothermal bulk moduli, and ρ is density.
are the adiabatic and isothermal bulk moduli, and ρ is density.
Microscopic definition via the phonon frequencies
The physical meaning of the parameter can also be extended by combining thermodynamics with a reasonable microphysics model for the vibrating atoms within a crystal. When the restoring force acting on an atom displaced from its equilibrium position is linear in the atom's displacement, the frequencies ωi of individual phonons do not depend on the volume of the crystal or on the presence of other phonons, and the thermal expansion (and thus γ) is zero. When the restoring force is non-linear in the displacement, the phonon frequencies ωi change with the volume  . The Grüneisen parameter of an individual vibrational mode
. The Grüneisen parameter of an individual vibrational mode  can then be defined as (the negative of) the logarithmic derivative of the corresponding frequency
can then be defined as (the negative of) the logarithmic derivative of the corresponding frequency 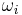 :
:
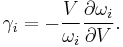
Relationship between microscopic and thermodynamic models
Using the quasi-harmonic approximation for atomic vibrations, the macroscopic Grüneisen parameter (γ) can be related to the description of how the vibration frequencies (phonons) within a crystal are altered with changing volume (i.e. γi's). For example, one can show that
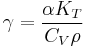
if one defines  as the weighted average
as the weighted average
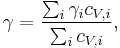
where 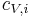 's are the partial vibrational mode contributions to the heat capacity, such that
's are the partial vibrational mode contributions to the heat capacity, such that 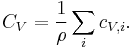
Derivation
To arrive at this result, one can start from the definitions of the two key quantities,
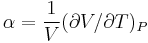 and
and 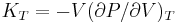 ,
,
by noting that 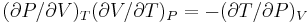 and thus
and thus
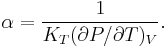
To calculate the partial derivative in this equation, let us first relate  to the internal energy
to the internal energy  . Writing the thermodynamic relationship
. Writing the thermodynamic relationship 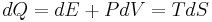 as
as
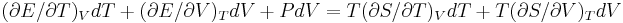 ,
,
we conclude that
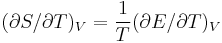 , and
, and ![(\partial S/\partial V)_T = \frac{1}{T} [ P %2B (\partial E/\partial V)_T ]](/2012-wikipedia_en_all_nopic_01_2012/I/63ac9af84d9deb4dc7434886f17650ce.png) .
.
Using 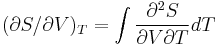 ,
,
we find the relationship between  and
and  :
:
![P(T) =
- \frac({\partial E}{\partial V})_T %2B
T \int_0^T \frac{1}{T^\prime} \frac{\partial^2 E }{\partial V \partial T^\prime} d T^\prime =
- \frac{\partial}{\partial V}[
E(T) - T \int_0^T \frac{1}{T^\prime} (\frac{\partial E(T^\prime) }{\partial T^\prime})_V d T^\prime
]_T.](/2012-wikipedia_en_all_nopic_01_2012/I/ac8fbf31714a0d7543651dde1fa00363.png)
The derivative 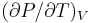 can then be calculated, resulting in
can then be calculated, resulting in
![\alpha =
\frac{1}{
K_T
\frac{\partial}{\partial V}
[ \int_0^T \frac{1}{T^\prime} (\frac{\partial E(T^\prime) }{\partial T^\prime})_V d T^\prime ]_T
}.](/2012-wikipedia_en_all_nopic_01_2012/I/93195fb025daf0ec965b5fc56d3cd332.png)
We can now express the latter partial derivatine via the parameters of the quasi-harmonic model. The internal energy is related to the vibrational mode frequencies 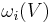 via
via
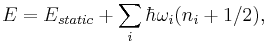
where 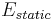 is the equilibrium energy of the lattice, and
is the equilibrium energy of the lattice, and 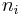 is the statistical occupation of the
is the statistical occupation of the  's mode, given by the Bose-Einstein distribution,
's mode, given by the Bose-Einstein distribution, ![n_i=\frac{1}{\exp[-\omega_i/T]-1}](/2012-wikipedia_en_all_nopic_01_2012/I/41d3e929ad441ad3b5c5176c16b48af1.png) . Since the only value that depends on the volume are the frequencies
. Since the only value that depends on the volume are the frequencies 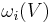 , the heat capacity per unit volume is
, the heat capacity per unit volume is
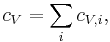 where
where
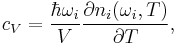
and the principal heat capacity is 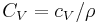 . The expression for
. The expression for  then reduces to
then reduces to
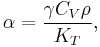
where by definition
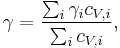
yielding the required relationship.
See also
External links
Gruneisen parameter has no units
References
- ^ E. Grüneisen, The state of a body. Handb. Phys., 10, 1-52. NASA translation RE2-18-59W